So why does the code produced in the last exercise contain the labels .LBB0_2 and .LBB0_3 but no .LBB0_1?

Well that is because I have added a code generation pass that deletes useless jumps like:

    	JNC .LBB0_1
    .LBB0_1:

Code snippets:

void HP41MCODEPassConfig::addPreEmitPass() {
    addPass(new RemoveUselessJMP()); }

...

bool RemoveUselessJMP::runOnMachineBasicBlock(
    MachineBasicBlock &MBB, MachineBasicBlock &MBBN) {
  bool Modified = false;

  MachineBasicBlock::iterator I = MBB.end();
  if (I != MBB.begin())
    I--;
  else
    return Modified;

  if (I->getOpcode() == HP41MCODE::JNC &&
        I->getOperand(0).getMBB() == &MBBN) {
    MBB.erase(I);
    Modified = true;
  }

  return Modified;
}

bool RemoveUselessJMP::runOnMachineFunction(MachineFunction &MF) {
  bool Modified = false;
  MachineFunction::iterator FJ = MF.begin();
  if (FJ != MF.end())
    FJ++;
  if (FJ == MF.end())
    return Modified;
  for (MachineFunction::iterator FI = MF.begin(),
       FE = MF.end(); FJ != FE; ++FI, ++FJ)
    Modified |= runOnMachineBasicBlock(*FI, *FJ);
 
  return Modified;
}

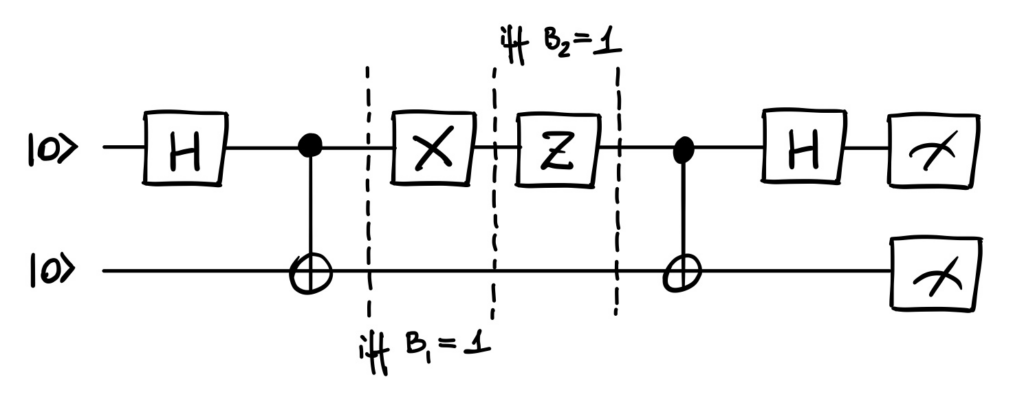
It is time to bring in some conditionals. Adding an “if” to our friend foo():

    int foo() {
      int retval1 = 0x0AB;
      int retval2 = 0;
      if (retval2)
        return retval2;
      return retval1;
    }

We need to implement instructions for both conditional and unconditional branches (i.e jumps). An unconditional branch is just like this (assuming no carry flag is set):

    ...

    def brtarget : Operand;
    
    ...
    
    let isBarrier=1, isBranch=1, isTerminator=1 in
    {
    def JNC : HP41MCODEInst<0x00B, (outs), (ins brtarget:$addr),
                            "JNC $addr", [(br bb:$addr)]>;
    }

We will use custom lowered pseudo instructions as an easy solution. This is a start:

    class HP41MCODEPseudo pattern> : HP41MCODEInst<0, outs, ins,
        asmstr, pattern> {
      let isCodeGenOnly = 1;
      let isPseudo = 1;
    }

    ...

    SDT_HP41MCODEBRCC : SDTypeProfile<0, 4, [SDTCisVT<0,
                                             OtherVT>]>;
    
    def HP41MCODEBRCC     : SDNode<"HP41MCODEISD::BRCC",
            SDT_HP41MCODEBRCC, [SDNPHasChain, SDNPInGlue]>;

    ...
    
    let isBranch=1, isTerminator=1 in
    {
    def BRCC : HP41MCODEPseudo< (outs), (ins brtarget:$addr,
            RC:$lhs, i32imm:$rhs, i32imm:$cond),
            "#BRCC $addr $lhs $rhs $cond",
            [(HP41MCODEBRCC bb:$addr, RC:$lhs, (i32 imm:$rhs),
             (i32 imm:$cond))]>;
    }

Note that this instruction will only match the case we have in this example. Different cases should use different instructions. More code snippets:

    ...

      BRCC,        // Branch to dest on condition
          
    ...
          
    SDValue LowerBR_CC(SDValue Op, SelectionDAG &DAG) const;

    ...
      
    setOperationAction(ISD::BR_CC, MVT::i32, Custom);
      
    ...
      
      case HP41MCODEISD::BRCC: return "HP41MCODEISD::BRCC";
      
    ...
    
    SDValue HP41MCODETargetLowering::LowerBR_CC(SDValue Op,
            SelectionDAG &DAG) const {
      SDValue Chain = Op.getOperand(0);
      ISD::CondCode CC = cast(Op.getOperand(1))->get();
      SDValue LHS = Op.getOperand(2);
      SDValue RHS = Op.getOperand(3);
      SDValue Dest = Op.getOperand(4);
      SDLoc dl(Op);

      return DAG.getNode(HP41MCODEISD::BRCC, dl, MVT::Other,
              Chain, Dest, LHS, RHS,
              DAG.getConstant(CC, dl, MVT::i32));
    }
    
    ...

      case ISD::BR_CC:
        return LowerBR_CC(Op, DAG);
    

So for this example we only need to produce machine instructions that compares the C register to 0 and then branches if it is equal. This must be done in a post-RA pass:

    bool HP41MCODEInstrInfo::expandPostRAPseudo(
          MachineInstr &MI) const {
      MachineBasicBlock &MBB = *MI.getParent();
      MachineFunction &MF = *MBB.getParent();
      const HP41MCODEInstrInfo &TII = *static_cast(
          MF.getSubtarget().getInstrInfo());
      DebugLoc dl = MBB.findDebugLoc(MI);

      switch (MI.getOpcode()) {
      case HP41MCODE::BRCC: {
        assert(MI.getOperand(1).getReg() == HP41MCODE::C &&
               "Not implemented!");
        assert(MI.getOperand(2).getImm() == 0 &&
               "Not implemented!");
        assert(MI.getOperand(3).getImm() == ISD::SETEQ &&
               "Not implemented!");

        BuildMI(MBB, MI, dl, TII.get(HP41MCODE::qCneq0ALL));
        BuildMI(MBB, MI, dl,
                TII.get(HP41MCODE::JNC)).addMBB(
                        MI.getOperand(0).getMBB());
        MI.eraseFromParent();
        return true;
      }
      }
      return false;
    }

This is the machine instruction used:

    def qCneq0ALL : HP41MCODEInst<0x2EE, (outs), (ins),
                                  "?C!=0 ALL", []>;

And we get:

	.file	"hello.c"
	.text
	.globl	foo                     ! -- Begin function foo
	.type	foo,@function
foo:                                    ! @foo
! %bb.0:                                ! %entry
	LDI S&X HEX: 0AB
	WRIT 2
	C=0 ALL
	WRIT 1
	READ 1
	?C!=0 ALL
	JNC .LBB0_2
! %bb.1:                                ! %if.then
	READ 1
	WRIT 3
	JNC .LBB0_3
.LBB0_2:                                ! %if.end
	READ 2
	WRIT 3
.LBB0_3:                                ! %return
	READ 3
	RTN
.Lfunc_end0:
	.size	foo, .Lfunc_end0-foo
                                        ! -- End function
	.ident	"clang version 20.0.0git (https://github.com/llvm/llvm-project.git ea1dfd50bfdfbd75969fd7653bc71c81f2a2350f)"
	.section	".note.GNU-stack"
	.addrsig

Let us add some local variables:

int foo() {
  int retval = 0x0AB;
  int dummy = 0;
  return retval;
}

This requires adding some information about accessing memory. I will just postulate that I have memory available from address 1 growing upwards. As anyone that really knows the HP-41 understands, this is a very bad idea. However we are still just showing some basic LLVM principles, not producing actually useful Nut code. I am however excluding the possibility of generating READ 0, as that instruction does not even exist.

Some code snippets:

    // Addressing modes.
    def ADDR : ComplexPattern<iPTR, 2, "SelectADDR",
                              [frameindex], []>;

    // Address operands
    def MEM : Operand {
      let MIOperandInfo = (ops RC, i16imm);
      let PrintMethod = "printMemOperand";
      let DecoderMethod = "decodeMemOperand";
    }
    
    ...
    
    let mayLoad=1 in {
    def READ : HP41MCODEInst<0x078, (outs RC:$r),
            (ins MEM:$addr), "READ $addr",
            [(set RC:$r, (load ADDR:$addr))]>;
    }

    let mayStore=1 in {
    def WRIT : HP41MCODEInst<0x068, (outs), (ins MEM:$addr,
            RC:$r), "WRIT $addr", [(store RC:$r, ADDR:$addr)]>;
    }

    ...

    bool
    HP41MCODERegisterInfo::eliminateFrameIndex(
            MachineBasicBlock::iterator II,
            int SPAdj, unsigned FIOperandNum,
            RegScavenger *RS) const {
        MachineInstr &MI = *II;
        int FrameIndex = MI.getOperand(FIOperandNum).getIndex();
        MachineFunction &MF = *MI.getParent()->getParent();
        const HP41MCODEFrameLowering *TFI = getFrameLowering(MF);
        llvm::Register FrameReg;
        int Offset;
        Offset = TFI->getFrameIndexReference(MF, FrameIndex,
                FrameReg).getFixed()/4+1;
        MI.getOperand(FIOperandNum).ChangeToRegister(FrameReg,
                false);
        MI.getOperand(FIOperandNum + 1).ChangeToImmediate(Offset);
        return false;
    }

    ...

    void HP41MCODEInstPrinter::printMemOperand(const MCInst *MI,
            int opNum,
            const MCSubtargetInfo &STI,
            raw_ostream &O, const char *Modifier) {
        const MCOperand &MO = MI->getOperand(opNum+1);
        
        if (MO.isImm()) {
            O << format_decimal((int)MO.getImm(), 1); return; }
                    assert(MO.isExpr() &&
                    "Unknown operand kind in printMemOperand");
                    MO.getExpr()->print(O, &MAI);
    }

    ...

    bool HP41MCODEDAGToDAGISel::SelectADDR(SDValue Addr,
            SDValue &Base, SDValue &Offset) {
      if (FrameIndexSDNode *FIN = dyn_cast(Addr)) {
        Base = CurDAG->getTargetFrameIndex(
                FIN->getIndex(), TLI->getPointerTy(
                        CurDAG->getDataLayout()));
        Offset = CurDAG->getTargetConstant(0, SDLoc(Addr),
                        MVT::i32);
        return true;
      }

      return false;
    }

Then we end up with:

	.file	"hello.c"
	.text
	.globl	foo                     ! -- Begin function foo
	.type	foo,@function
foo:                                    ! @foo
! %bb.0:                                ! %entry
	LDI S&X HEX: 0AB
	WRIT 2
	C=0 ALL
	WRIT 1
	READ 2
	RTN
.Lfunc_end0:
	.size	foo, .Lfunc_end0-foo
                                        ! -- End function
	.ident	"clang version 20.0.0git (https://github.com/llvm/llvm-project.git ea1dfd50bfdfbd75969fd7653bc71c81f2a2350f)"
	.section	".note.GNU-stack"
	.addrsig

How about calling another function:

int foo() {
    return 0xFF;
}

int bar() {
    return foo();
}

Code snippets:

...

def CC_HP41MCODE : CallingConv<[]>;

...

def SDT_HP41MCODENCXQ : SDTypeProfile<0, -1,
                                      [SDTCisVT<0, iPTR>]>;
def HP41MCODENCXQ : SDNode<"HP41MCODEISD::NCXQ",
                           SDT_HP41MCODENCXQ,
                           [SDNPHasChain, SDNPOptInGlue,
                            SDNPOutGlue, SDNPVariadic]>;

...

def calltarget : Operand;

...

let isCall=1 in {
    def NCXQ : HP41MCODEInst<0x001, (outs),
                             (ins calltarget:$addr),
                             "?NC XQ $addr",
                             [(HP41MCODENCXQ
                              tglobaladdr:$addr)]>;
}

...

NCXQ,         // A call instruction.

...

SDValue
HP41MCODETargetLowering::LowerCall(
        TargetLowering::CallLoweringInfo &CLI,
        SmallVectorImpl &InVals) const {
    ...

    CCInfo.AnalyzeCallOperands(Outs, CC_HP41MCODE);

    ...

    Chain = DAG.getNode(HP41MCODEISD::NCXQ, DL, NodeTys, Ops);

    ...

    return Chain;
}

...

The following assembly is produced:

	.file	"hello.c"
	.text
	.globl	foo                     ! -- Begin function foo
	.type	foo,@function
foo:                                    ! @foo
! %bb.0:                                ! %entry
	LDI S&X HEX: 0FF
	RTN
.Lfunc_end0:
	.size	foo, .Lfunc_end0-foo
                                        ! -- End function
	.globl	bar                     ! -- Begin function bar
	.type	bar,@function
bar:                                    ! @bar
! %bb.0:                                ! %entry
	?NC XQ foo
	RTN
.Lfunc_end1:
	.size	bar, .Lfunc_end1-bar
                                        ! -- End function
	.ident	"clang version 20.0.0git (https://github.com/llvm/llvm-project.git ea1dfd50bfdfbd75969fd7653bc71c81f2a2350f)"
	.section	".note.GNU-stack"
	.addrsig
	.addrsig_sym foo

This is sort of the opposite of the Quantum Teleportation we have covered earlier. Here you use quantum bits to transfer classical bits:

We have all the building blocks we need from the previous episode, so let me just show you the additional code:

#Alice bits
a1=1
a2=1
print("Alice bits:",a1,a2)

#Initialize inputs
q=[[1],[0],[0],[0]]

#Build circuit
U=kron(H,I)
U=mult(CNOT,U)

#Encode bits
if a2==1:
  U=mult(kron(X,I),U)
if a1==1:
  U=mult(kron(Z,I),U)

#Run circuit
q=mult(U,q)

#Bob applies gates
q=mult(CNOT,q)
q=mult(kron(H,I),q)

#Bob measurements
b1=qbit(0,M(q))
q=qbitset(0,b1,q)
b2=qbit(1,M(q))
q=qbitset(1,b2,q)

print("Bob measurements:",b1,b2)

So as an example we try to give Bob the bits 1 and 1. Bob does his measurements and this is the result:

Let us return a larger constant:

int foo() {
    return 0xFF;
}

For numbers up to 12 bits we can use the LDI S&X instruction. Some code snippets:

def immSExt12 : PatLeaf<(imm),
                    [{ return isInt<12>(N->getSExtValue()); }]>;

def : Pat<(i32 immSExt12:$in), (LDI imm:$in)>;

def LDI : HP41MCODEInst<0x130, (outs RC:$r), (ins i32imm:$sx),
                        "LDI S&X HEX: $sx",
                        [(set RC:$r, (i32 immSExt12:$sx))]>;

This produces:

	.file	"hello.c"
	.text
	.globl	foo                     ! -- Begin function foo
	.type	foo,@function
foo:                                    ! @foo
! %bb.0:                                ! %entry
	LDI S&X HEX: 0FF
	RTN
.Lfunc_end0:
	.size	foo, .Lfunc_end0-foo
                                        ! -- End function
	.ident	"clang version 20.0.0git (https://github.com/llvm/llvm-project.git ea1dfd50bfdfbd75969fd7653bc71c81f2a2350f)"
	.section	".note.GNU-stack"
	.addrsig

A tiny addition to the empty function. Returning zero:

int foo() {
    return 0;
}

Remember, we will not care about returning values to the calculator registers (at not least for now). We will only generate functions callable from MCODE. So as a convention we will choose to return values in the C register.

So we will need an instruction to load 0 into the C register:

def Ceq0ALL : HP41MCODEInst<0x04E, (outs RC:$r), (ins),
                            "C=0 ALL", [(set RC:$r, 0)]>;

This replacement pattern will make sure a constant 0 is loaded with this instruction:

def : Pat<(i32 0), (Ceq0ALL)>;

A register class for just this register (the instruction is only used with the C register, i.e. implicit addressing):

def RC : RegisterClass<"HP41MCODE", [i32], 8, (add C)>;

Defining the calling convention to return values in the C register:

def RetCC_HP41MCODE : CallingConv<[
      CCAssignToReg<[C]>
    ]>;

Adding this calling convention to the LowerReturn() function mentioned earlier, to analyze returns:

SDValue
HP41MCODETargetLowering::LowerReturn(SDValue Chain,
        CallingConv::ID CallConv,
        bool IsVarArg,
        const SmallVectorImpl &Outs,
        const SmallVectorImpl &OutVals,
        const SDLoc &DL, SelectionDAG &DAG) const {
  ...
  // Analyze return values.
  CCInfo.AnalyzeReturn(Outs, RetCC_HP41MCODE);
  ...
  return DAG.getNode(HP41MCODEISD::RTN, DL, MVT::Other, RetOps);
}

That gives us this MCODE assembly:

	.file	"hello.c"
	.text
	.globl	foo                     ! -- Begin function foo
	.type	foo,@function
foo:                                    ! @foo
! %bb.0:                                ! %entry
	C=0 ALL
	RTN
.Lfunc_end0:
	.size	foo, .Lfunc_end0-foo
                                        ! -- End function
	.ident	"clang version 20.0.0git (https://github.com/llvm/llvm-project.git ea1dfd50bfdfbd75969fd7653bc71c81f2a2350f)"
	.section	".note.GNU-stack"
	.addrsig

How to make a compiler? As an exercise I have already threatened to produce at least some assembly code for the Nut CPU used in the HP-41 calculator. There will be huge compromises (it is after all just an exercise):

1. I will copy and strip down an existing compiler backend in the LLVM project, then build some small parts up again with Nut code and new naming. This is also what the LLVM documentation recommends. I will start with Sparc as they suggest. To connect the new backend with clang all the Sparc stuff in that subproject must also be copied and renamed. This is actually not a small task, it takes like a week or so to do all of this and to get everything up building and running again…
2. I will not care about assembler directives in the source code, I will at least for now just stay with the format inherited from the compiler backend I took as a starting point.
3. I will not care much about about the calculator itself, just the CPU. Although I technically could produce something that could be assembled with the A41 assembler (see the SDK documentation) and run as a proper calculator function in the corresponding emulator, this is just too cumbersome at least from the very start. I do not have the hardware needed to run my own MCODE in the physical machine… I will just produce some code for a hypothetical standalone CPU running in hex mode. Actual calculator registers contain floating point numbers encoded as BCD…

So what does it take? We should probably start by defining some registers:

//===-- HP41MCODERegisterInfo.td - HP41MCODE Register defs -*- tablegen -*-===//
//
// Part of the LLVM Project, under the Apache License v2.0 with LLVM Exceptions.
// See https://llvm.org/LICENSE.txt for license information.
// SPDX-License-Identifier: Apache-2.0 WITH LLVM-exception
//
//===----------------------------------------------------------------------===//

//===----------------------------------------------------------------------===//
//  Declarations that describe the HP41MCODE register file
//===----------------------------------------------------------------------===//

class HP41MCODEReg<bits<16> Enc, string n> : Register {
  let HWEncoding = Enc;
  let Namespace = "HP41MCODE";
}

def A   : HP41MCODEReg< 1, "A">;
def B   : HP41MCODEReg< 2, "B">;
def C   : HP41MCODEReg< 3, "C">;

def R56 : RegisterClass<"HP41MCODE", [i32], 8, (add A, B, C )>;

For simplicity in this exercise I will only use 32 of the 56 bits in the registers, to make it easier for modern compiler infrastructure…

But what is the simplest function we can generate code for? It must be this:

void foo() {
    return;
}

For this we just need a return instruction. Some code snippets:

...

namespace HP41MCODEISD {
    enum NodeType : unsigned {
      ...
      RTN,         // A return instruction.
      ...
    };
  }

...

SDValue
HP41MCODETargetLowering::LowerReturn(SDValue Chain,
        CallingConv::ID CallConv,
        bool IsVarArg,
        const SmallVectorImpl &Outs,
        const SmallVectorImpl &OutVals,
        const SDLoc &DL, SelectionDAG &DAG) const {
  ...
  return DAG.getNode(HP41MCODEISD::RTN, DL, MVT::Other, RetOps);
}

const char *HP41MCODETargetLowering::getTargetNodeName(
        unsigned Opcode) const {
  switch ((HP41MCODEISD::NodeType)Opcode) {
  ...
  case HP41MCODEISD::RTN: return "HP41MCODEISD::RTN";
  ...
  }
  return nullptr;
}

...

def HP41MCODERTN : SDNode<"HP41MCODEISD::RTN", SDTNone,
                          [SDNPHasChain, SDNPOptInGlue, SDNPVariadic]>;
...

let isReturn=1, isTerminator=1, isBarrier=1 in {

def RTN : HP41MCODEInst<0x3E0, (outs), (ins), "RTN",
                        [(HP41MCODERTN)]>;

}

...

So what does that produce? A function that just returns, but in MCODE assembly… I realize this is a very small step for humanity, but it is a giant leap for someone just starting to learn about LLVM:

	.file	"hello.c"
	.text
	.globl	foo                     ! -- Begin function foo
	.type	foo,@function
foo:                                    ! @foo
! %bb.0:                                ! %entry
	RTN
.Lfunc_end0:
	.size	foo, .Lfunc_end0-foo
                                        ! -- End function
	.ident	"clang version 20.0.0git (https://github.com/llvm/llvm-project.git 1a75416092746b127fb7cfec3fcbe37ab765da58)"
	.section	".note.GNU-stack"
	.addrsig

The HP-41 calculators can be programmed with microcode, aka MCODE. This is how their normal instructions are implemented. The emulator even has an MCODE console where  you can step though its instructions. On the physical machine running your own MCODE requires making ROMs (or something that pretends to be a ROM…). I am not familiar with how this works with the emulator, but I have found an SDK.

Microcode is of course very low level so it could be interesting to compile e.g. C to MCODE. This is also so utterly useless that it would be insanely fun to at least make a tiny prototype or a starting point for such a compiler. Imagine creating e.g. MCODE assembly with clang/llvm:

./clang.exe --target=hp41 -S hello.c